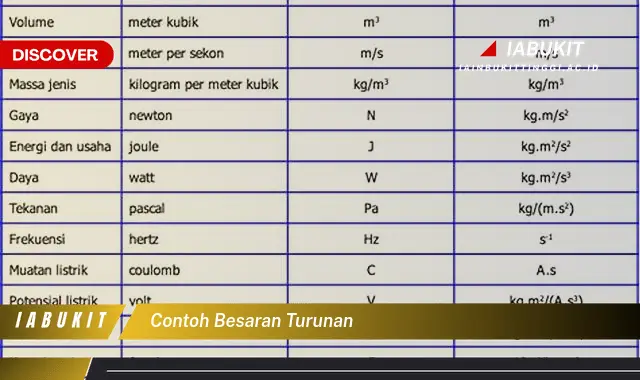
Besaran turunan adalah besaran yang diturunkan dari besaran pokok. Besaran pokok adalah besaran yang ditetapkan terlebih dahulu dan tidak dapat diturunkan dari besaran lainnya, seperti panjang, massa, dan waktu. Sedangkan besaran turunan adalah besaran yang diperoleh dari hasil perkalian, pembagian, atau kombinasi dari besaran pokok. Contoh besaran turunan adalah kecepatan, percepatan, dan gaya.
Besaran turunan sangat penting dalam fisika karena dapat digunakan untuk menghitung dan mengukur berbagai besaran fisika. Misalnya, kecepatan dapat dihitung dengan membagi jarak dengan waktu, dan percepatan dapat dihitung dengan membagi perubahan kecepatan dengan waktu. Besaran turunan juga memiliki satuan yang diturunkan dari satuan besaran pokok. Misalnya, satuan kecepatan adalah meter per sekon (m/s), dan satuan percepatan adalah meter per sekon kuadrat (m/s).
Dalam fisika, terdapat tujuh besaran pokok yang menjadi dasar dari seluruh besaran fisika lainnya. Ketujuh besaran pokok tersebut adalah panjang, massa, waktu, suhu, intensitas cahaya, jumlah zat, dan kuat arus listrik. Sementara itu, besaran turunan sangat banyak jumlahnya dan dapat dibagi menjadi beberapa kategori, seperti besaran mekanika, besaran termodinamika, dan besaran elektromagnetik.
Contoh Besaran Turunan
Besaran turunan adalah besaran yang diturunkan dari besaran pokok. Besaran pokok adalah besaran yang ditetapkan terlebih dahulu dan tidak dapat diturunkan dari besaran lainnya, seperti panjang, massa, dan waktu. Sedangkan besaran turunan adalah besaran yang diperoleh dari hasil perkalian, pembagian, atau kombinasi dari besaran pokok. Berikut adalah 7 aspek penting terkait contoh besaran turunan:
- Jenis besaran turunan
- Satuan besaran turunan
- Rumus besaran turunan
- Contoh besaran turunan dalam kehidupan sehari-hari
- Penggunaan besaran turunan dalam fisika
- Manfaat besaran turunan
- Sejarah besaran turunan
Besaran turunan sangat penting dalam fisika karena dapat digunakan untuk menghitung dan mengukur berbagai besaran fisika. Misalnya, kecepatan dapat dihitung dengan membagi jarak dengan waktu, dan percepatan dapat dihitung dengan membagi perubahan kecepatan dengan waktu. Besaran turunan juga memiliki satuan yang diturunkan dari satuan besaran pokok. Misalnya, satuan kecepatan adalah meter per sekon (m/s), dan satuan percepatan adalah meter per sekon kuadrat (m/s^2).
Jenis Besaran Turunan
Besaran turunan dapat dibagi menjadi beberapa jenis, antara lain:
.
- Besaran mekanika, seperti kecepatan, percepatan, gaya, usaha, dan energi.
- Besaran termodinamika, seperti suhu, kalor, dan entropi.
- Besaran elektromagnetik, seperti medan listrik, medan magnet, dan fluks magnetik.
- Besaran kimia, seperti konsentrasi, pH, dan laju reaksi.
- Besaran optik, seperti intensitas cahaya, panjang gelombang, dan frekuensi.
Jenis besaran turunan sangat beragam dan terus berkembang seiring dengan perkembangan ilmu pengetahuan dan teknologi.
Satuan Besaran Turunan
Satuan besaran turunan adalah satuan yang diturunkan dari satuan besaran pokok. Satuan besaran pokok adalah satuan yang ditetapkan terlebih dahulu dan tidak dapat diturunkan dari satuan lainnya, seperti meter, kilogram, dan sekon. Sedangkan satuan besaran turunan adalah satuan yang diperoleh dari hasil perkalian, pembagian, atau kombinasi dari satuan besaran pokok.
- Cara penulisan satuan besaran turunan
Penulisan satuan besaran turunan mengikuti aturan perkalian dan pembagian satuan besaran pokok. Misalnya, satuan kecepatan adalah meter per sekon (m/s), yang diperoleh dari perkalian satuan panjang (meter) dengan satuan waktu (sekon).
- Contoh satuan besaran turunan
Beberapa contoh satuan besaran turunan antara lain:
- Kecepatan (m/s)
- Percepatan (m/s^2)
- Gaya (N)
- Usaha (J)
- Daya (W)
- Penggunaan satuan besaran turunan
Satuan besaran turunan digunakan untuk mengukur berbagai besaran fisika. Misalnya, satuan kecepatan (m/s) digunakan untuk mengukur kecepatan benda, satuan gaya (N) digunakan untuk mengukur gaya yang bekerja pada benda, dan satuan usaha (J) digunakan untuk mengukur usaha yang dilakukan pada benda.
- Hubungan satuan besaran turunan dengan besaran pokok
Satuan besaran turunan memiliki hubungan yang erat dengan satuan besaran pokok. Satuan besaran turunan dapat diturunkan dari satuan besaran pokok melalui operasi matematika seperti perkalian, pembagian, pangkat, dan akar.
Dengan memahami satuan besaran turunan, kita dapat mengukur dan menyatakan besaran fisika secara akurat dan konsisten. Satuan besaran turunan sangat penting dalam berbagai bidang ilmu pengetahuan dan teknologi, termasuk fisika, kimia, dan teknik.
Rumus Besaran Turunan
Rumus besaran turunan adalah persamaan matematika yang digunakan untuk menghitung nilai besaran turunan dari besaran pokok. Rumus besaran turunan sangat penting karena memungkinkan kita untuk menghitung berbagai besaran fisika yang tidak dapat diukur secara langsung.
Sebagai contoh, rumus kecepatan adalah jarak dibagi waktu (v = s/t). Rumus ini menunjukkan bahwa kecepatan dapat dihitung dengan membagi jarak yang ditempuh oleh benda dengan waktu yang dibutuhkan untuk menempuh jarak tersebut. Contoh lainnya, rumus gaya adalah massa dikalikan percepatan (F = m*a). Rumus ini menunjukkan bahwa gaya yang bekerja pada benda dapat dihitung dengan mengalikan massa benda dengan percepatannya.
Rumus besaran turunan dapat diturunkan dari hukum-hukum dasar fisika. Misalnya, rumus kecepatan dapat diturunkan dari hukum gerak Newton pertama, yang menyatakan bahwa percepatan suatu benda berbanding lurus dengan gaya yang bekerja pada benda dan berbanding terbalik dengan massanya. Rumus gaya dapat diturunkan dari hukum gerak Newton kedua, yang menyatakan bahwa percepatan suatu benda berbanding lurus dengan gaya yang bekerja pada benda dan berbanding terbalik dengan massanya.
Dengan memahami rumus besaran turunan, kita dapat menghitung dan mengukur berbagai besaran fisika secara akurat dan konsisten. Rumus besaran turunan sangat penting dalam berbagai bidang ilmu pengetahuan dan teknologi, termasuk fisika, kimia, dan teknik.
Contoh Besaran Turunan dalam Kehidupan Sehari-hari
Besaran turunan memiliki peran penting dalam kehidupan sehari-hari kita. Berbagai besaran yang kita gunakan dan ukur dalam kegiatan sehari-hari merupakan besaran turunan. Berikut adalah beberapa contoh besaran turunan dalam kehidupan sehari-hari:
- Kecepatan kendaraan bermotor
- Waktu tempuh perjalanan
- Konsumsi bahan bakar kendaraan
- Luas permukaan ruangan
- Volume air dalam botol
- Berat badan seseorang
- Suhu udara
- Intensitas cahaya lampu
- Kekuatan arus listrik
- Tekanan udara dalam ban
Besaran-besaran turunan tersebut sangat penting dalam berbagai aspek kehidupan kita, seperti transportasi, perdagangan, kesehatan, dan teknologi. Dengan memahami konsep besaran turunan, kita dapat mengukur dan mengelola berbagai aspek kehidupan kita secara lebih akurat dan efisien.
Penggunaan Besaran Turunan dalam Fisika
Besaran turunan sangat penting dalam fisika karena digunakan untuk mengukur dan menghitung berbagai besaran fisika. Tanpa besaran turunan, kita tidak dapat mengukur besaran-besaran seperti kecepatan, percepatan, gaya, usaha, dan energi. Besaran-besaran ini sangat penting dalam memahami dan menjelaskan fenomena alam.
Sebagai contoh, dalam mekanika, besaran turunan seperti kecepatan dan percepatan digunakan untuk menghitung gaya yang bekerja pada benda. Dalam termodinamika, besaran turunan seperti suhu dan kalor digunakan untuk menghitung perubahan energi internal suatu sistem. Dalam elektromagnetisme, besaran turunan seperti medan listrik dan medan magnet digunakan untuk menghitung gaya yang bekerja pada muatan listrik dan arus listrik.
Dengan memahami penggunaan besaran turunan dalam fisika, kita dapat menganalisis dan memprediksi berbagai fenomena alam. Hal ini sangat penting dalam pengembangan teknologi dan kemajuan ilmu pengetahuan pada umumnya.
Manfaat Besaran Turunan
Besaran turunan memiliki banyak manfaat dalam berbagai bidang ilmu pengetahuan dan teknologi. Berikut adalah beberapa manfaat besaran turunan:
- Memudahkan Pengukuran
Besaran turunan memudahkan kita untuk mengukur besaran fisika yang tidak dapat diukur secara langsung. Misalnya, kita tidak dapat mengukur kecepatan secara langsung, tetapi kita dapat menghitungnya dengan membagi jarak yang ditempuh dengan waktu yang dibutuhkan.
- Menghitung Besaran Fisika Lainnya
Besaran turunan dapat digunakan untuk menghitung besaran fisika lainnya. Misalnya, kita dapat menghitung gaya yang bekerja pada benda dengan mengalikan massa benda dengan percepatannya.
- Membuat Model Matematika
Besaran turunan dapat digunakan untuk membuat model matematika yang menggambarkan fenomena alam. Misalnya, kita dapat membuat model matematika untuk menghitung lintasan gerak benda dengan menggunakan besaran turunan seperti kecepatan dan percepatan.
- Mengembangkan Teknologi
Besaran turunan sangat penting dalam pengembangan teknologi. Misalnya, besaran turunan seperti gaya dan tekanan digunakan dalam desain dan pembuatan mesin dan struktur.
Dengan memahami manfaat besaran turunan, kita dapat memanfaatkannya untuk berbagai keperluan dalam ilmu pengetahuan dan teknologi. Besaran turunan membantu kita memahami dunia sekitar dan mengembangkan teknologi baru yang bermanfaat bagi kehidupan manusia.
Sejarah Besaran Turunan
Sejarah besaran turunan tidak dapat dipisahkan dari perkembangan ilmu fisika itu sendiri. Sejak zaman dahulu, manusia telah menggunakan besaran-besaran untuk mengukur dan memahami dunia sekitar. Namun, konsep besaran turunan baru berkembang secara sistematis pada abad ke-17 dan ke-18, seiring dengan kemajuan pesat dalam bidang mekanika dan matematika.
Pada awalnya, para ilmuwan menggunakan besaran-besaran pokok seperti panjang, massa, dan waktu untuk mengukur besaran fisika lainnya. Namun, seiring dengan berkembangnya ilmu pengetahuan, para ilmuwan menyadari bahwa banyak besaran fisika yang tidak dapat diukur secara langsung menggunakan besaran-besaran pokok saja. Hal inilah yang mendorong pengembangan konsep besaran turunan.
Besaran turunan pertama kali diperkenalkan oleh fisikawan Italia Galileo Galilei pada abad ke-17. Galileo menggunakan konsep kecepatan, yang merupakan besaran turunan dari panjang dan waktu, untuk mempelajari gerak benda. Konsep kecepatan kemudian dikembangkan lebih lanjut oleh Isaac Newton pada abad ke-18, yang juga memperkenalkan konsep-konsep turunan lainnya seperti percepatan dan gaya.
Pada abad ke-19 dan ke-20, konsep besaran turunan terus berkembang dan diperluas. Para ilmuwan mengembangkan besaran-besaran turunan baru untuk mengukur berbagai besaran fisika, seperti suhu, energi, dan medan elektromagnetik. Perkembangan ini sangat penting dalam kemajuan ilmu fisika dan teknologi.
Dengan memahami sejarah besaran turunan, kita dapat lebih mengapresiasi pentingnya konsep ini dalam ilmu fisika. Besaran turunan memungkinkan kita untuk mengukur dan memahami berbagai fenomena alam yang kompleks. Konsep ini juga sangat penting dalam pengembangan teknologi baru yang bermanfaat bagi kehidupan manusia.
Pertanyaan yang Sering Diajukan tentang Besaran Turunan
Berikut adalah beberapa pertanyaan yang sering diajukan tentang besaran turunan, beserta jawabannya:
Pertanyaan 1: Apa yang dimaksud dengan besaran turunan?
Besaran turunan adalah besaran yang diturunkan dari besaran pokok. Besaran pokok adalah besaran yang ditetapkan terlebih dahulu dan tidak dapat diturunkan dari besaran lainnya, seperti panjang, massa, dan waktu. Sedangkan besaran turunan adalah besaran yang diperoleh dari hasil perkalian, pembagian, atau kombinasi dari besaran pokok.
Pertanyaan 2: Apa saja contoh besaran turunan?
Ada banyak sekali contoh besaran turunan, seperti kecepatan, percepatan, gaya, usaha, energi, suhu, dan intensitas cahaya.
Pertanyaan 3: Apa manfaat besaran turunan?
Besaran turunan memiliki banyak manfaat, antara lain memudahkan pengukuran, menghitung besaran fisika lainnya, membuat model matematika, dan mengembangkan teknologi.
Pertanyaan 4: Bagaimana sejarah perkembangan besaran turunan?
Konsep besaran turunan pertama kali diperkenalkan oleh Galileo Galilei pada abad ke-17. Konsep ini kemudian dikembangkan lebih lanjut oleh Isaac Newton dan para ilmuwan lainnya pada abad-abad berikutnya.
Dengan memahami besaran turunan dan manfaatnya, kita dapat memanfaatkannya untuk berbagai keperluan dalam ilmu pengetahuan dan teknologi. Besaran turunan membantu kita memahami dunia sekitar dan mengembangkan teknologi baru yang bermanfaat bagi kehidupan manusia.
Baca juga: Rumus dan Satuan Besaran Turunan
Tips Memahami Besaran Turunan
Besaran turunan sangat penting dalam fisika karena memungkinkan kita mengukur dan menghitung berbagai besaran fisika yang tidak dapat diukur secara langsung. Untuk memahami konsep besaran turunan dengan lebih baik, berikut adalah beberapa tips:
Tip 1: Pahami besaran pokok terlebih dahulu
Besaran pokok adalah besaran dasar yang tidak dapat diturunkan dari besaran lain. Memahami besaran pokok akan membantu Anda memahami bagaimana besaran turunan diturunkan.Tip 2: Pelajari rumus besaran turunan
Setiap besaran turunan memiliki rumus yang berbeda. Pelajari rumus-rumus ini agar Anda dapat menghitung besaran turunan dengan benar.Tip 3: Berlatih soal-soal besaran turunan
Cara terbaik untuk menguasai konsep besaran turunan adalah dengan berlatih soal-soal. Carilah soal-soal latihan dan cobalah selesaikan sendiri.Tip 4: Gunakan satuan besaran turunan dengan benar
Setiap besaran turunan memiliki satuan yang berbeda. Pastikan Anda menggunakan satuan yang benar saat menghitung atau mengukur besaran turunan.Tip 5: Hubungkan besaran turunan dengan konsep fisika lainnya
Besaran turunan saling berhubungan dengan konsep fisika lainnya. Misalnya, kecepatan berhubungan dengan jarak dan waktu. Dengan memahami hubungan ini, Anda akan lebih mudah memahami konsep-konsep fisika secara keseluruhan.Dengan mengikuti tips-tips ini, Anda dapat memahami konsep besaran turunan dengan lebih baik. Pemahaman yang baik tentang besaran turunan akan membantu Anda dalam mempelajari fisika dan memecahkan masalah-masalah fisika yang melibatkan besaran turunan.
Dengan memahami besaran turunan, kita dapat mengukur dan memahami dunia sekitar kita dengan lebih akurat. Besaran turunan sangat penting dalam berbagai bidang ilmu pengetahuan dan teknologi, seperti fisika, kimia, dan teknik.
Youtube Video: