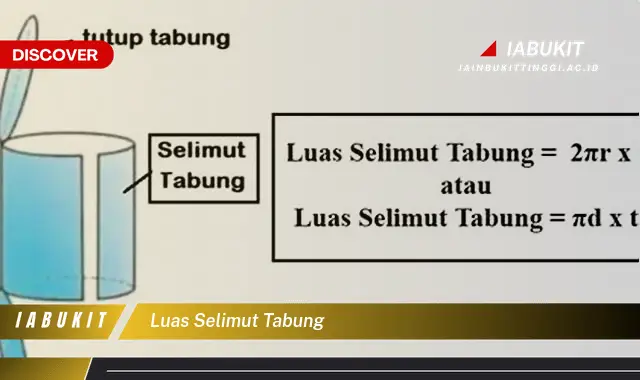
Luas selimut tabung adalah ukuran luas permukaan lengkung tabung. Rumus untuk menghitung luas selimut tabung adalah 2r x t, di mana r adalah jari-jari alas tabung dan t adalah tinggi tabung.
Luas selimut tabung penting dalam berbagai aplikasi, seperti menghitung volume tabung dan menghitung luas permukaan benda-benda yang berbentuk tabung. Luas selimut tabung juga digunakan dalam bidang teknik dan desain industri untuk menghitung luas permukaan benda-benda yang berputar, seperti pipa dan silinder.
Secara historis, konsep luas selimut tabung pertama kali dikembangkan oleh matematikawan Yunani Archimedes pada abad ke-3 SM. Archimedes menggunakan konsep ini untuk menghitung volume tabung dan bola.
Luas Selimut Tabung
Luas selimut tabung merupakan aspek penting dalam geometri dan memiliki berbagai aplikasi dalam kehidupan nyata. Berikut adalah 7 aspek penting terkait luas selimut tabung:
- Rumus: 2r x t
- Satuan: cm2 atau m2
- Aplikasi: Menghitung volume tabung
- Aplikasi: Menghitung luas permukaan benda berbentuk tabung
- Sejarah: Dikembangkan oleh Archimedes
- Konsep: Luas permukaan lengkung tabung
- Pentingnya: Digunakan dalam teknik dan desain industri
Dengan memahami aspek-aspek penting ini, kita dapat lebih memahami konsep luas selimut tabung dan mengaplikasikannya dengan baik. Misalnya, dalam menghitung volume tabung, kita perlu mengetahui luas selimut tabung dan tinggi tabung. Selain itu, luas selimut tabung juga digunakan dalam menghitung luas permukaan benda-benda berbentuk tabung, seperti pipa dan silinder.
Rumus
Rumus 2r x t digunakan untuk menghitung luas selimut tabung, yaitu ukuran luas permukaan lengkung tabung. Rumus ini memiliki beberapa aspek penting:
- Komponen:
r: jari-jari alas tabung
t: tinggi tabung
- Aplikasi:
Menghitung luas selimut tabung
Menghitung volume tabung
Menghitung luas permukaan benda berbentuk tabung
- Contoh:
Sebuah tabung memiliki jari-jari alas 5 cm dan tinggi 10 cm. Maka luas selimut tabung tersebut adalah 2 x 5 cm x 10 cm = 100 cm2.
- Implikasi:
Rumus ini menunjukkan bahwa luas selimut tabung berbanding lurus dengan jari-jari alas dan tinggi tabung.
Rumus ini penting dalam berbagai aplikasi teknik dan desain industri, seperti menghitung luas permukaan pipa dan silinder.
Dengan memahami rumus 2r x t, kita dapat menghitung luas selimut tabung dengan mudah dan akurat. Rumus ini menjadi dasar untuk berbagai aplikasi penting dalam matematika, fisika, dan teknik.
Satuan
Dalam konteks luas selimut tabung, satuan yang digunakan untuk menyatakan luas tersebut adalah cm2 atau m2. Pemilihan satuan tergantung pada ukuran dan konteks penggunaan tabung.
- Satuan cm2:
Satuan cm2 (sentimeter persegi) digunakan untuk menyatakan luas selimut tabung yang berukuran kecil atau sedang, seperti tabung reaksi atau kaleng minuman.
- Satuan m2:
Satuan m2 (meter persegi) digunakan untuk menyatakan luas selimut tabung yang berukuran besar, seperti pipa atau tangki penyimpanan.
Penggunaan satuan yang tepat dalam menyatakan luas selimut tabung sangat penting untuk memastikan akurasi dan konsistensi dalam perhitungan dan aplikasi.
Aplikasi
Luas selimut tabung memiliki hubungan yang erat dengan volume tabung. Volume tabung dapat dihitung menggunakan rumus V = L x t, di mana V adalah volume tabung, L adalah luas selimut tabung, dan t adalah tinggi tabung.
- Komponen:
Luas selimut tabung (L)
Tinggi tabung (t)
- Contoh:
Sebuah tabung memiliki luas selimut 100 cm2 dan tinggi 10 cm. Maka volume tabung tersebut adalah 100 cm2 x 10 cm = 1000 cm3.
- Implikasi:
Rumus ini menunjukkan bahwa volume tabung berbanding lurus dengan luas selimut tabung dan tinggi tabung.
Rumus ini digunakan dalam berbagai aplikasi teknik dan desain industri, seperti menghitung volume pipa dan tangki penyimpanan.
Dengan memahami hubungan antara luas selimut tabung dan volume tabung, kita dapat menghitung volume tabung dengan mudah dan akurat. Rumus ini menjadi dasar untuk berbagai aplikasi penting dalam matematika, fisika, dan teknik.
Aplikasi
Luas selimut tabung merupakan komponen penting dalam menghitung luas permukaan benda berbentuk tabung. Luas permukaan benda berbentuk tabung terdiri dari luas selimut tabung dan dua kali luas alas tabung. Dengan demikian, untuk menghitung luas permukaan benda berbentuk tabung, kita perlu mengetahui luas selimut tabung.
Contohnya, sebuah pipa berbentuk tabung memiliki jari-jari alas 5 cm dan tinggi 10 cm. Luas selimut tabung tersebut adalah 2 x x 5 cm x 10 cm = 100 cm2. Untuk menghitung luas permukaan pipa tersebut, kita perlu menambahkan dua kali luas alas, yaitu 2 x x 5 cm x 5 cm = 50 cm2. Jadi, luas permukaan pipa tersebut adalah 100 cm2 + 50 cm2 = 150 cm2.
Dengan memahami hubungan antara luas selimut tabung dan luas permukaan benda berbentuk tabung, kita dapat menghitung luas permukaan benda-benda tersebut dengan mudah dan akurat. Perhitungan ini penting dalam berbagai aplikasi, seperti desain industri, teknik sipil, dan arsitektur.
Sejarah
Konsep luas selimut tabung tidak terlepas dari sejarah perkembangan matematika. Archimedes, seorang matematikawan Yunani yang hidup pada abad ke-3 SM, memainkan peran penting dalam pengembangan konsep ini.
- Penemuan Rumus: Archimedes menemukan rumus untuk menghitung luas selimut tabung, yaitu 2r x t, di mana adalah konstanta matematika, r adalah jari-jari alas tabung, dan t adalah tinggi tabung.
- Aplikasi dalam Mengukur Volume: Penemuan rumus luas selimut tabung memungkinkan Archimedes untuk mengembangkan metode untuk mengukur volume tabung. Metode ini menjadi dasar bagi perkembangan kalkulus integral di kemudian hari.
- Pengaruh pada Matematika: Karya Archimedes tentang luas selimut tabung menjadi landasan penting bagi perkembangan geometri dan kalkulus. Rumus yang ia temukan masih digunakan hingga sekarang untuk menghitung luas selimut tabung.
Dengan memahami sejarah pengembangan konsep luas selimut tabung, kita dapat mengapresiasi pentingnya konsep ini dalam matematika dan penerapannya dalam berbagai bidang ilmu pengetahuan.
Konsep
Konsep luas permukaan lengkung tabung merupakan bagian fundamental dari luas selimut tabung. Luas permukaan lengkung tabung adalah luas permukaan tabung yang melengkung, tidak termasuk luas kedua alas tabung. Dalam konteks tabung, permukaan lengkung tersebut berbentuk persegi panjang, dengan panjang keliling alas tabung dan tinggi tabung sebagai lebarnya.
Luas permukaan lengkung tabung berperan penting dalam menghitung luas selimut tabung karena luas selimut tabung merupakan penjumlahan dari luas permukaan lengkung tabung dan dua kali luas alas tabung. Dengan memahami konsep luas permukaan lengkung tabung, kita dapat memahami bagaimana luas selimut tabung dihitung dan diaplikasikan dalam berbagai bidang.
Pentingnya
Luas selimut tabung memegang peranan penting dalam teknik dan desain industri karena berperan sebagai komponen krusial dalam berbagai perhitungan dan aplikasi. Dalam bidang teknik, luas selimut tabung digunakan untuk menghitung luas permukaan benda-benda berbentuk tabung, seperti pipa, tangki, dan silinder. Perhitungan ini sangat penting untuk menentukan kebutuhan material, efisiensi desain, dan performa struktural.
Selain itu, dalam desain industri, luas selimut tabung digunakan untuk mengoptimalkan bentuk dan estetika produk. Misalnya, dalam desain kemasan, luas selimut tabung digunakan untuk menentukan ukuran dan bentuk wadah yang paling efisien dan menarik. Dengan memahami luas selimut tabung, desainer dapat menciptakan produk yang fungsional, estetis, dan sesuai dengan kebutuhan pasar.
Pertanyaan Umum tentang Luas Selimut Tabung
Berikut adalah beberapa pertanyaan umum tentang luas selimut tabung beserta jawabannya:
Pertanyaan 1: Apa itu luas selimut tabung?
Jawaban: Luas selimut tabung adalah ukuran luas permukaan lengkung tabung, yaitu luas permukaan tabung yang tidak termasuk luas kedua alasnya.
Pertanyaan 2: Bagaimana cara menghitung luas selimut tabung?
Jawaban: Luas selimut tabung dapat dihitung menggunakan rumus 2r x t, di mana r adalah jari-jari alas tabung dan t adalah tinggi tabung.
Pertanyaan 3: Apa saja aplikasi luas selimut tabung?
Jawaban: Luas selimut tabung memiliki berbagai aplikasi, antara lain dalam menghitung volume tabung, menghitung luas permukaan benda berbentuk tabung, dan dalam teknik dan desain industri.
Pertanyaan 4: Mengapa luas selimut tabung penting dalam teknik dan desain industri?
Jawaban: Luas selimut tabung penting dalam teknik dan desain industri karena digunakan untuk menghitung luas permukaan benda berbentuk tabung, seperti pipa, tangki, dan silinder. Perhitungan ini sangat penting untuk menentukan kebutuhan material, efisiensi desain, dan performa struktural.
Dengan memahami konsep dan aplikasi luas selimut tabung, kita dapat memanfaatkannya untuk berbagai keperluan dalam matematika, fisika, teknik, dan desain industri.
Berikutnya: Rumus Luas Selimut Tabung
Tips Menghitung Luas Selimut Tabung
Berikut adalah beberapa tips untuk menghitung luas selimut tabung dengan mudah dan akurat:
Tip 1: Pastikan Anda mengetahui jari-jari alas (r) dan tinggi tabung (t) dengan benar.
Tip 2: Gunakan rumus yang tepat untuk menghitung luas selimut tabung, yaitu 2r x t.
Tip 3: Perhatikan satuan yang digunakan, baik sentimeter (cm) atau meter (m), dan pastikan konsistensi satuan.
Tip 4: Jika memungkinkan, buat sketsa tabung untuk memvisualisasikan dan memahami konsep luas selimut tabung.
Tip 5: Latih soal-soal yang berkaitan dengan luas selimut tabung untuk meningkatkan pemahaman dan keterampilan.
Dengan mengikuti tips ini, Anda dapat menghitung luas selimut tabung secara efektif dan memperoleh pemahaman yang baik tentang konsep ini.
Selain tips di atas, penting untuk memahami konsep dasar tabung, seperti jari-jari alas, tinggi, dan luas permukaan. Pemahaman yang komprehensif akan membantu Anda menguasai perhitungan luas selimut tabung dan menerapkannya dalam berbagai situasi.
Youtube Video: