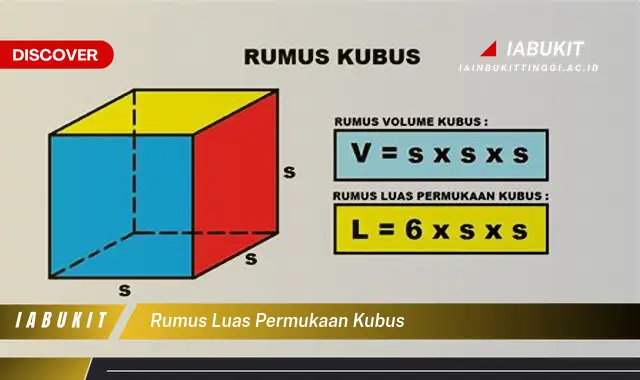
Rumus luas permukaan kubus adalah rumus yang digunakan untuk menghitung luas permukaan suatu kubus. Rumus ini dapat digunakan untuk menghitung luas permukaan kubus dengan berbagai ukuran. Misalnya, jika sebuah kubus memiliki panjang rusuk 5 cm, maka luas permukaannya adalah 6 x 52 = 150 cm2.
Rumus luas permukaan kubus sangat penting dalam berbagai bidang, seperti arsitektur, teknik, dan desain. Rumus ini dapat digunakan untuk menghitung luas permukaan bangunan, benda-benda, dan objek lainnya yang berbentuk kubus. Selain itu, rumus ini juga dapat digunakan untuk menghitung volume kubus, yaitu dengan mengalikan luas permukaan kubus dengan tinggi kubus.
Rumus luas permukaan kubus pertama kali ditemukan oleh matematikawan Yunani kuno, Archimedes, pada abad ke-3 SM. Archimedes menggunakan rumus ini untuk menghitung luas permukaan sebuah bola. Sejak saat itu, rumus ini telah banyak digunakan dalam berbagai bidang dan menjadi salah satu rumus matematika yang paling dasar dan penting.
Rumus Luas Permukaan Kubus
Rumus luas permukaan kubus merupakan konsep penting yang digunakan untuk menghitung luas permukaan kubus. Rumus ini memiliki berbagai aspek penting yang perlu dipahami.
- Kubus: Bangun ruang tiga dimensi yang dibatasi oleh enam bidang berbentuk persegi.
- Luas permukaan: Total luas seluruh permukaan suatu bangun ruang.
- Rumus: 6 x (sisi x sisi), di mana “sisi” adalah panjang rusuk kubus.
- Aplikasi: Menghitung luas permukaan kubus dalam bidang arsitektur, teknik, dan desain.
- Sejarah: Ditemukan oleh Archimedes pada abad ke-3 SM.
- Volume: Dapat dihitung dengan mengalikan luas permukaan kubus dengan tingginya.
- Satuan: Luas permukaan kubus biasanya dinyatakan dalam satuan meter persegi (m2) atau sentimeter persegi (cm2).
Memahami aspek-aspek tersebut sangat penting untuk menguasai konsep rumus luas permukaan kubus. Rumus ini menjadi dasar dalam berbagai bidang dan memiliki keterkaitan erat dengan konsep matematika lainnya, seperti volume dan luas permukaan bangun ruang lainnya.
Kubus
Kubus merupakan bangun ruang tiga dimensi yang memiliki enam bidang berbentuk persegi. Setiap sisi kubus memiliki ukuran yang sama, baik panjang maupun lebarnya. Bentuk kubus yang teratur ini menjadikannya mudah untuk dianalisis dan dihitung luas permukaannya.
Rumus luas permukaan kubus didasarkan pada struktur kubus yang memiliki enam bidang berbentuk persegi. Rumus tersebut, yaitu 6 x (sisi x sisi), merupakan perkalian dari luas permukaan satu sisi kubus dengan jumlah seluruh sisinya. Dengan demikian, rumus ini dapat digunakan untuk menghitung luas permukaan kubus dengan mudah dan akurat.
Hubungan antara definisi kubus dan rumus luas permukaan kubus sangatlah erat. Definisi kubus memberikan gambaran tentang bentuk dan struktur bangun ruang, sedangkan rumus luas permukaan kubus merupakan metode matematis yang digunakan untuk menghitung luas permukaan bangun ruang tersebut berdasarkan bentuknya yang teratur.
Luas permukaan
Dalam konteks rumus luas permukaan kubus, memahami konsep luas permukaan sangatlah penting. Luas permukaan merupakan besaran yang menyatakan ukuran seluruh permukaan suatu bangun ruang. Dalam hal kubus, luas permukaan mewakili jumlah luas seluruh bidang persegi yang membentuk kubus tersebut.
- Komponen Luas Permukaan Kubus
Luas permukaan kubus terdiri dari enam bidang persegi yang sama luas. Setiap bidang persegi tersebut memiliki luas yang dihitung menggunakan rumus L = s x s, dengan s adalah panjang sisi persegi. - Aplikasi Praktis
Konsep luas permukaan kubus memiliki banyak aplikasi praktis, seperti dalam arsitektur dan teknik. Misalnya, untuk menghitung luas permukaan dinding sebuah ruangan berbentuk kubus atau menghitung luas permukaan sebuah benda berbentuk kubus. - Rumus Luas Permukaan Kubus
Rumus luas permukaan kubus, yaitu 6 x (sisi x sisi), diturunkan dari konsep luas permukaan dan sifat kubus yang memiliki enam bidang persegi sama luas. Rumus ini digunakan untuk menghitung total luas permukaan kubus berdasarkan panjang sisinya. - Hubungan dengan Volume Kubus
Luas permukaan kubus juga memiliki hubungan dengan volume kubus. Volume kubus dapat dihitung dengan mengalikan luas permukaan kubus dengan tinggi kubus. Hubungan ini menunjukkan keterkaitan antara ukuran permukaan dan kapasitas suatu kubus.
Dengan memahami hubungan antara luas permukaan dan rumus luas permukaan kubus, kita dapat memperoleh pemahaman yang lebih mendalam tentang sifat-sifat kubus dan penerapannya dalam berbagai bidang.
Rumus
Rumus ini merupakan rumus yang digunakan untuk menghitung luas permukaan kubus. Rumus ini diturunkan dari konsep luas permukaan dan sifat-sifat kubus. Berikut adalah beberapa aspek penting dari rumus tersebut:
- Komponen Rumus
Rumus ini terdiri dari beberapa komponen, yaitu:- 6: Angka ini menunjukkan jumlah sisi kubus.
- (sisi x sisi): Bagian ini mewakili luas permukaan satu sisi kubus. Panjang sisi kubus dikuadratkan karena setiap sisi dianggap sebagai persegi.
- Aplikasi Praktis
Rumus ini memiliki banyak aplikasi praktis, seperti:- Menghitung luas permukaan dinding ruangan berbentuk kubus.
- Menghitung luas permukaan kemasan berbentuk kubus.
- Menghitung luas permukaan benda-benda berbentuk kubus lainnya.
- Hubungan dengan Sifat Kubus
Rumus ini terkait dengan sifat-sifat kubus, yaitu:- Kubus memiliki enam sisi berbentuk persegi.
- Semua sisi kubus memiliki luas yang sama.
Dengan memahami rumus dan sifat-sifat kubus, kita dapat menghitung luas permukaan kubus secara akurat dan memahami implikasinya dalam berbagai aplikasi praktis.
Aplikasi
Rumus luas permukaan kubus memiliki peran penting dalam berbagai aplikasi praktis, khususnya dalam bidang arsitektur, teknik, dan desain. Rumus ini digunakan untuk menghitung luas permukaan benda-benda atau struktur yang berbentuk kubus.
- Arsitektur
Dalam arsitektur, rumus luas permukaan kubus digunakan untuk menghitung luas permukaan dinding, lantai, dan langit-langit ruangan yang berbentuk kubus. Hal ini penting untuk menentukan kebutuhan material, seperti cat, wallpaper, atau ubin, serta memperkirakan biaya pembangunan. - Teknik
Dalam teknik, rumus luas permukaan kubus digunakan untuk menghitung luas permukaan benda-benda berbentuk kubus, seperti tangki air, balok beton, atau kemasan produk. Informasi ini penting untuk menentukan kapasitas, kekuatan, dan efisiensi benda-benda tersebut. - Desain
Dalam desain, rumus luas permukaan kubus digunakan untuk menghitung luas permukaan benda-benda dekoratif atau fungsional yang berbentuk kubus, seperti lampu, meja, atau rak. Hal ini membantu desainer menentukan ukuran, proporsi, dan estetika benda-benda tersebut.
Dengan memahami rumus luas permukaan kubus dan penerapannya dalam bidang-bidang tersebut, kita dapat menghargai pentingnya konsep ini dalam dunia nyata dan melihat bagaimana matematika berperan dalam membentuk lingkungan dan objek yang kita gunakan sehari-hari.
Sejarah
Penemuan rumus luas permukaan kubus oleh Archimedes pada abad ke-3 SM menjadi tonggak penting dalam sejarah matematika. Penemuan ini membuka jalan bagi pemahaman yang lebih mendalam tentang sifat-sifat kubus dan aplikasinya dalam berbagai bidang.
- Asal-usul dan Perkembangan
Rumus luas permukaan kubus ditemukan oleh Archimedes sebagai bagian dari karyanya dalam mengukur volume dan luas permukaan bangun ruang. Penemuan ini didasarkan pada prinsip-prinsip geometri dan aljabar yang sudah ada pada saat itu. - Pengakuan dan Pengaruh
Rumus Archimedes segera mendapat pengakuan dan digunakan secara luas oleh matematikawan dan ilmuwan pada zaman kuno dan abad pertengahan. Rumus ini menjadi dasar bagi pengembangan konsep luas permukaan dan volume bangun ruang lainnya. - Aplikasi Praktis
Rumus luas permukaan kubus memiliki banyak aplikasi praktis, seperti dalam arsitektur, teknik, dan desain. Rumus ini digunakan untuk menghitung luas permukaan benda-benda atau struktur yang berbentuk kubus, seperti dinding, lantai, dan kemasan. - Signifikansi Historis
Penemuan rumus luas permukaan kubus oleh Archimedes menunjukkan kecerdasan dan kemampuan matematika yang luar biasa. Rumus ini telah bertahan selama berabad-abad dan terus digunakan hingga saat ini, menjadi bukti keabadian kontribusi Archimedes pada ilmu pengetahuan.
Dengan memahami sejarah penemuan rumus luas permukaan kubus, kita dapat mengapresiasi pentingnya konsep ini dan menyadari bagaimana matematika telah berkembang seiring waktu melalui karya para ilmuwan dan matematikawan terkemuka seperti Archimedes.
Volume
Rumus volume kubus memiliki keterkaitan yang erat dengan rumus luas permukaan kubus. Volume suatu kubus dihitung dengan mengalikan luas permukaan kubus dengan tinggi kubus. Hubungan ini menunjukkan bahwa luas permukaan kubus merupakan komponen penting dalam menentukan volume kubus.
Dengan memahami hubungan ini, kita dapat memperoleh pemahaman yang lebih komprehensif tentang sifat-sifat kubus dan hubungan antara luas permukaan dan volume suatu bangun ruang. Rumus luas permukaan kubus menjadi dasar untuk menghitung volume kubus, yang pada gilirannya memberikan informasi tentang kapasitas atau ukuran suatu kubus.
Satuan
Satuan luas permukaan kubus merupakan komponen penting dalam rumus luas permukaan kubus karena satuan ini menunjukkan besaran luas permukaan yang dihitung. Penggunaan satuan yang tepat memastikan bahwa hasil perhitungan luas permukaan kubus dapat dipahami dan dibandingkan dengan benar.
Pemilihan satuan luas permukaan kubus, seperti meter persegi (m2) atau sentimeter persegi (cm2), bergantung pada konteks dan kebutuhan. Dalam bidang arsitektur dan konstruksi, misalnya, meter persegi (m2) umum digunakan untuk menyatakan luas permukaan dinding, lantai, atau langit-langit sebuah ruangan. Sementara itu, sentimeter persegi (cm2) lebih sering digunakan untuk menyatakan luas permukaan benda-benda yang lebih kecil, seperti kemasan produk atau alas sebuah meja.
Dengan memahami pentingnya satuan dalam rumus luas permukaan kubus, kita dapat memastikan bahwa perhitungan yang dilakukan akurat dan sesuai dengan kebutuhan pengukuran.
Tanya Jawab Umum
Berikut adalah beberapa pertanyaan umum dan jawabannya terkait dengan rumus luas permukaan kubus:
Pertanyaan 1: Bagaimana cara menghitung luas permukaan kubus?
Jawaban: Luas permukaan kubus dapat dihitung menggunakan rumus 6 x (sisi x sisi), di mana “sisi” adalah panjang rusuk kubus.
Pertanyaan 2: Apa satuan yang biasa digunakan untuk menyatakan luas permukaan kubus?
Jawaban: Satuan yang umum digunakan untuk menyatakan luas permukaan kubus adalah meter persegi (m2) dan sentimeter persegi (cm2).
Pertanyaan 3: Apa saja aplikasi praktis dari rumus luas permukaan kubus?
Jawaban: Rumus luas permukaan kubus memiliki banyak aplikasi praktis, seperti menghitung luas permukaan dinding, lantai, dan langit-langit dalam arsitektur, menghitung luas permukaan kemasan produk dalam desain, dan menghitung luas permukaan benda-benda berbentuk kubus lainnya dalam berbagai bidang.
Pertanyaan 4: Bagaimana rumus luas permukaan kubus berkaitan dengan volume kubus?
Jawaban: Volume kubus dapat dihitung dengan mengalikan luas permukaan kubus dengan tinggi kubus. Hubungan ini menunjukkan keterkaitan antara luas permukaan dan volume kubus.
Dengan memahami pertanyaan dan jawaban umum ini, kita dapat memperoleh pemahaman yang lebih baik tentang konsep luas permukaan kubus dan penerapannya dalam berbagai bidang.
Catatan: Pertanyaan dan jawaban dalam FAQ ini hanya mencakup beberapa pertanyaan umum. Untuk pertanyaan atau informasi lebih lanjut, disarankan untuk berkonsultasi dengan sumber terpercaya atau pakar di bidang terkait.
Kembali ke Artikel Utama
Tips Menghitung Luas Permukaan Kubus
Berikut adalah beberapa tips untuk membantu Anda menghitung luas permukaan kubus dengan mudah dan akurat:
Tip 1: Identifikasi Sisi Kubus
Sebelum menghitung luas permukaan kubus, pastikan Anda mengetahui panjang sisi kubus. Panjang sisi adalah ukuran dari salah satu rusuk penyusun kubus.
Tip 2: Gunakan Rumus yang Tepat
Gunakan rumus luas permukaan kubus yang benar, yaitu 6 x (sisi x sisi). Dalam rumus ini, “sisi” mewakili panjang sisi kubus.
Tip 3: Kuadratkan Panjang Sisi
Dalam rumus luas permukaan kubus, panjang sisi harus dikuadratkan. Artinya, panjang sisi dikalikan dengan dirinya sendiri.
Tip 4: Kalikan dengan 6
Setelah mengkuadratkan panjang sisi, kalikan hasilnya dengan 6. Angka 6 mewakili jumlah sisi kubus.
Tip 5: Pilih Satuan yang Tepat
Jangan lupa untuk menyatakan luas permukaan kubus dalam satuan yang tepat, seperti meter persegi (m2) atau sentimeter persegi (cm2).
Dengan mengikuti tips ini, Anda dapat menghitung luas permukaan kubus dengan percaya diri dan akurat.
Kesimpulan
Memahami dan menerapkan rumus luas permukaan kubus sangat penting dalam berbagai bidang. Dengan memahami tips yang telah diuraikan, Anda dapat menghitung luas permukaan kubus dengan mudah dan tepat, sehingga memberikan dasar yang kuat untuk aplikasi praktis dalam arsitektur, teknik, dan bidang lainnya.
Youtube Video: