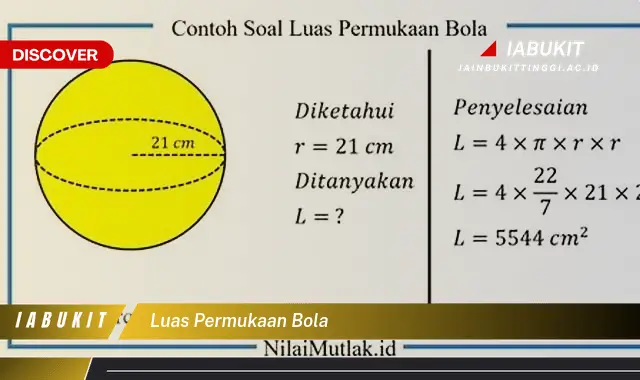
Luas permukaan bola adalah ukuran total luas permukaan bola. Dengan kata lain, ini adalah luas total semua titik pada permukaan bola. Untuk menghitung luas permukaan bola, kita dapat menggunakan rumus berikut: L = 4r, di mana L adalah luas permukaan, dan r adalah jari-jari bola.
Luas permukaan bola penting karena dapat digunakan untuk menghitung volume bola, serta untuk menyelesaikan masalah yang berkaitan dengan luas permukaan bola. Misalnya, jika kita tahu jari-jari bola, kita dapat menggunakan rumus luas permukaan bola untuk menghitung luas total permukaan bola tersebut.
Konsep luas permukaan bola telah digunakan selama berabad-abad, dan telah menjadi bagian penting dari matematika dan fisika. Konsep ini pertama kali dikembangkan oleh Archimedes pada abad ke-3 SM, dan sejak itu telah digunakan oleh para ilmuwan dan matematikawan untuk menyelesaikan berbagai masalah.
Luas Permukaan Bola
Luas permukaan bola adalah besaran yang penting dalam matematika dan fisika, dengan berbagai aspek krusial yang saling berhubungan.
- Rumus: 4r, di mana r adalah jari-jari bola.
- Satuan: Satuan luas, seperti meter persegi (m).
- Aplikasi: Menghitung volume bola, luas permukaan benda bulat.
- Sejarah: Ditemukan oleh Archimedes pada abad ke-3 SM.
- Sifat: Selalu positif, berbanding lurus dengan kuadrat jari-jari.
- Hubungan: Terkait dengan luas lingkaran dan volume bola.
- Contoh: Bola dengan jari-jari 5 cm memiliki luas permukaan 314 cm.
Dengan memahami berbagai aspek ini, kita dapat memperoleh pemahaman yang lebih komprehensif tentang luas permukaan bola dan penerapannya dalam berbagai bidang.
Rumus
Rumus ini sangat penting dalam menghitung luas permukaan bola karena memberikan hubungan langsung antara jari-jari bola dan luas permukaannya. Dengan menggunakan rumus ini, kita dapat menentukan luas permukaan bola hanya dengan mengetahui jari-jarinya.
Rumus ini diturunkan berdasarkan prinsip-prinsip geometri dan kalkulus. Secara intuitif, kita dapat membayangkan bola sebagai kumpulan lingkaran dengan jari-jari yang sama, yang ditumpuk di atas satu sama lain. Luas permukaan setiap lingkaran adalah r, di mana r adalah jari-jari lingkaran. Dengan menjumlahkan luas permukaan semua lingkaran ini, kita mendapatkan luas permukaan bola, yang dinyatakan dalam rumus 4r.
Pemahaman yang kuat tentang rumus ini sangat penting untuk menyelesaikan masalah yang melibatkan luas permukaan bola. Dalam berbagai bidang seperti fisika, teknik, dan desain, menghitung luas permukaan bola merupakan tugas yang umum. Dengan menggunakan rumus ini secara efektif, kita dapat memperoleh hasil yang akurat dan andal.
Satuan
Satuan luas memainkan peran krusial dalam konteks luas permukaan bola. Luas permukaan bola diukur dan dinyatakan dalam satuan luas, seperti meter persegi (m). Satuan ini memberikan referensi yang jelas dan terstandarisasi untuk membandingkan dan mengukur luas permukaan bola yang berbeda.
- Konsistensi dan Perbandingan: Penggunaan satuan luas yang sama, seperti meter persegi, memastikan konsistensi dalam pengukuran luas permukaan bola. Ini memungkinkan kita untuk membandingkan luas permukaan bola yang berbeda secara akurat dan objektif.
- Aplikasi Praktis: Satuan luas seperti meter persegi memiliki aplikasi praktis yang luas. Dalam bidang arsitektur, teknik, dan desain, pengukuran luas permukaan bola dalam meter persegi sangat penting untuk perhitungan yang akurat, seperti menentukan kebutuhan material dan merencanakan tata letak ruang.
- Konteks Fisika: Dalam fisika, luas permukaan bola berperan penting dalam menghitung gaya hambat dan perpindahan panas. Mengekspresikan luas permukaan dalam satuan meter persegi memungkinkan integrasi yang mulus dengan persamaan dan model fisika lainnya.
- Standarisasi Internasional: Meter persegi adalah satuan luas yang diakui secara internasional, yang memfasilitasi komunikasi dan pertukaran informasi tentang luas permukaan bola di seluruh dunia.
Dengan demikian, satuan luas seperti meter persegi sangat penting untuk mengukur dan membandingkan luas permukaan bola secara konsisten dan akurat. Satuan ini memberikan dasar yang kokoh untuk aplikasi praktis, perhitungan fisika, dan kolaborasi internasional dalam bidang yang berkaitan dengan luas permukaan bola.
Aplikasi
Luas permukaan bola memiliki peran penting dalam menghitung volume bola dan luas permukaan benda bulat. Berikut penjelasannya:
- Volume Bola: Volume bola dapat dihitung menggunakan rumus V = (4/3)r, di mana r adalah jari-jari bola. Dalam rumus ini, luas permukaan bola (4r) berperan sangat penting karena merupakan faktor yang menentukan volume bola.
- Luas Permukaan Benda Bulat: Luas permukaan benda bulat, seperti silinder, kerucut, atau bola, sering kali melibatkan perhitungan luas permukaan bola. Misalnya, pada silinder, kedua alasnya berbentuk lingkaran, dan luas permukaan lingkaran tersebut merupakan komponen dari luas permukaan total silinder.
Oleh karena itu, memahami luas permukaan bola sangat penting dalam berbagai aplikasi, termasuk menghitung volume bola dan luas permukaan benda bulat. Dengan menghitung luas permukaan bola secara akurat, kita dapat menentukan volume dan luas permukaan benda bulat lainnya dengan tepat.
Sejarah
Penemuan luas permukaan bola oleh Archimedes pada abad ke-3 SM merupakan tonggak penting dalam sejarah matematika. Penemuan ini memberikan dasar bagi pengembangan kalkulus dan geometri modern, serta pemahaman yang lebih mendalam tentang bentuk dan ukuran benda bulat.
Archimedes menggunakan metode pemecahan masalah yang cerdik dan inovatif untuk menurunkan rumus luas permukaan bola. Metode ini melibatkan pembagian bola menjadi sejumlah kecil piramida dan kemudian menghitung luas permukaan setiap piramida. Dengan menjumlahkan luas permukaan semua piramida, Archimedes memperoleh rumus luas permukaan bola, yaitu 4r, di mana r adalah jari-jari bola.
Penemuan Archimedes memiliki dampak yang signifikan terhadap perkembangan matematika dan fisika. Rumus luas permukaan bola telah menjadi alat penting dalam berbagai bidang, mulai dari arsitektur hingga kedirgantaraan. Penemuan ini juga membuka jalan bagi penemuan-penemuan matematika lainnya, termasuk kalkulus integral dan konsep limit.
Sifat
Sifat luas permukaan bola yang selalu positif dan berbanding lurus dengan kuadrat jari-jari merupakan aspek krusial dalam memahami karakteristik dan perhitungan luas permukaan bola. Sifat ini memiliki beberapa implikasi penting:
- Kepositifan: Luas permukaan bola selalu bernilai positif atau nol. Hal ini mencerminkan sifat dasar luas permukaan sebagai besaran yang tidak dapat bernilai negatif. Sifat kepositifan ini sangat penting dalam aplikasi praktis, seperti menghitung volume dan luas permukaan benda bulat.
- Hubungan Kuadratik: Luas permukaan bola berbanding lurus dengan kuadrat jari-jari. Artinya, jika jari-jari bola diperbesar dua kali, luas permukaannya akan menjadi empat kali lebih besar. Hubungan kuadratik ini menunjukkan bahwa luas permukaan bola tumbuh lebih cepat daripada jari-jarinya, yang penting untuk dipertimbangkan dalam aplikasi yang melibatkan perubahan ukuran bola.
Memahami sifat luas permukaan bola sangat penting untuk melakukan perhitungan dan analisis yang akurat. Dengan mempertimbangkan kepositifan dan hubungan kuadratiknya, kita dapat memperoleh wawasan yang lebih dalam tentang perilaku luas permukaan bola dan menerapkannya secara efektif dalam berbagai bidang.
Hubungan
Luas permukaan bola memiliki hubungan yang erat dengan luas lingkaran dan volume bola. Hubungan ini sangat penting untuk memahami sifat dan aplikasi luas permukaan bola. Berikut penjelasannya:
- Luas Lingkaran: Luas permukaan bola terdiri dari banyak lingkaran kecil dengan jari-jari yang sama dengan jari-jari bola. Luas setiap lingkaran ini adalah r, di mana r adalah jari-jari bola. Dengan menjumlahkan luas semua lingkaran ini, kita memperoleh luas permukaan bola, yaitu 4r. Hubungan ini menunjukkan bahwa luas permukaan bola bergantung pada luas lingkaran yang membentuknya.
- Volume Bola: Volume bola dapat dihitung menggunakan rumus V = (4/3)r, di mana r adalah jari-jari bola. Dalam rumus ini, luas permukaan bola (4r) berperan penting karena merupakan faktor yang menentukan volume bola. Hubungan ini menunjukkan bahwa luas permukaan bola secara langsung memengaruhi volume bola.
Memahami hubungan antara luas permukaan bola, luas lingkaran, dan volume bola sangat penting untuk melakukan perhitungan dan analisis yang akurat. Dengan mempertimbangkan hubungan ini, kita dapat memperoleh wawasan yang lebih dalam tentang perilaku luas permukaan bola dan menerapkannya secara efektif dalam berbagai aplikasi.
Contoh
Contoh yang diberikan menyajikan sebuah ilustrasi konkret tentang hubungan antara luas permukaan bola dan jari-jarinya. Bola dengan jari-jari 5 cm memiliki luas permukaan 314 cm, yang merupakan hasil dari penerapan rumus luas permukaan bola (4r) dengan jari-jari r = 5 cm. Contoh ini menunjukkan bagaimana rumus luas permukaan bola dapat digunakan untuk menghitung luas permukaan bola dengan jari-jari tertentu.
Pertanyaan Umum tentang Luas Permukaan Bola
Bagian ini menyajikan beberapa pertanyaan umum beserta jawabannya terkait topik luas permukaan bola.
Pertanyaan 1: Bagaimana cara menghitung luas permukaan bola?
Luas permukaan bola dapat dihitung menggunakan rumus 4r, di mana r adalah jari-jari bola.
Pertanyaan 2: Apa satuan luas permukaan bola?
Satuan luas permukaan bola adalah satuan luas, seperti meter persegi (m) atau sentimeter persegi (cm).
Pertanyaan 3: Apa saja aplikasi luas permukaan bola dalam kehidupan nyata?
Luas permukaan bola memiliki berbagai aplikasi dalam bidang teknik, fisika, dan desain, seperti menghitung volume bola, menentukan luas permukaan benda bulat, dan merancang struktur kubah.
Pertanyaan 4: Siapa yang pertama kali menemukan rumus luas permukaan bola?
Rumus luas permukaan bola pertama kali ditemukan oleh Archimedes, seorang matematikawan Yunani kuno, pada abad ke-3 SM.
Dengan memahami pertanyaan umum ini dan jawabannya, kita dapat memperoleh pemahaman yang lebih baik tentang konsep luas permukaan bola dan penerapannya dalam berbagai bidang.
Baca Juga:
- Sejarah Perkembangan Rumus Luas Permukaan Bola
- Aplikasi Luas Permukaan Bola dalam Arsitektur
Tips Mengenai Luas Permukaan Bola
Untuk memahami dan mengaplikasikan konsep luas permukaan bola secara efektif, perhatikan beberapa tips berikut:
Tip 1: Pahami Rumus Secara Menyeluruh
Rumus luas permukaan bola, yaitu 4r, merupakan dasar untuk menghitung luas permukaan bola. Pastikan untuk memahami rumus ini dan cara menerapkannya dengan benar.
Tip 2: Perhatikan Satuan dengan Cermat
Luas permukaan bola dinyatakan dalam satuan luas, seperti meter persegi atau sentimeter persegi. Perhatikan satuan dengan cermat untuk memastikan konsistensi dan hasil perhitungan yang akurat.
Tip 3: Visualisasikan Bola Sebagai Kumpulan Lingkaran
Bola dapat dibayangkan sebagai kumpulan lingkaran dengan jari-jari yang sama. Luas permukaan setiap lingkaran berkontribusi pada luas permukaan bola secara keseluruhan. Visualisasi ini dapat membantu dalam memahami sifat luas permukaan bola.
Tip 4: Hubungkan dengan Konsep Volume Bola
Luas permukaan bola terkait erat dengan volume bola. Rumus volume bola melibatkan luas permukaan bola sebagai faktor. Dengan memahami hubungan ini, Anda dapat memperoleh wawasan yang lebih dalam tentang sifat-sifat bola.
Tip 5: Latih Soal dan Aplikasi Praktis
Untuk menguasai konsep luas permukaan bola, latihan soal dan penerapan praktis sangat penting. Carilah soal-soal latihan yang menantang dan terapkan konsep ini dalam skenario dunia nyata, seperti menghitung luas permukaan bola lampu atau mendesain struktur kubah.
Dengan mengikuti tips ini, Anda dapat meningkatkan pemahaman dan keterampilan Anda dalam bekerja dengan konsep luas permukaan bola.
Kesimpulan:
Luas permukaan bola merupakan konsep penting dalam matematika dan memiliki berbagai aplikasi dalam bidang sains dan teknik. Dengan memahami rumus, sifat, dan hubungannya, Anda dapat menguasai konsep ini dan menerapkannya secara efektif untuk memecahkan masalah dan memperoleh wawasan dalam berbagai bidang.
Youtube Video: