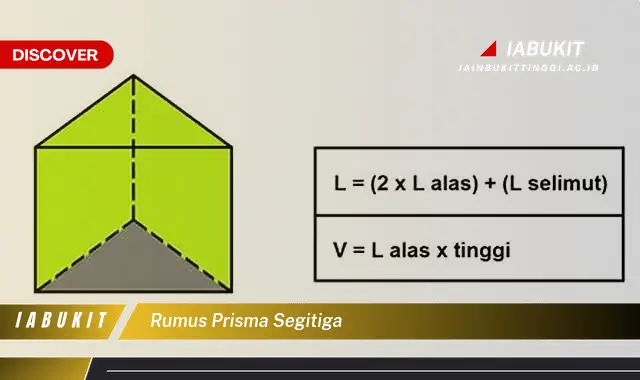
Rumus prisma segitiga adalah rumus untuk mencari volume dan luas permukaan prisma segitiga. Rumus volume prisma segitiga adalah V = 1/2 luas alas tinggi. Sedangkan rumus luas permukaan prisma segitiga adalah L = 2 (luas alas + luas selimut). Luas alas prisma segitiga adalah 1/2 a t, di mana a adalah panjang alas dan t adalah tinggi alas. Sedangkan luas selimut prisma segitiga adalah P t, di mana P adalah keliling alas dan t adalah tinggi prisma.
Rumus prisma segitiga sangat penting dalam matematika, khususnya dalam geometri ruang. Rumus ini digunakan untuk menghitung volume dan luas permukaan prisma segitiga, yang merupakan bangun ruang yang sering dijumpai dalam kehidupan sehari-hari. Selain itu, rumus prisma segitiga juga bermanfaat dalam bidang teknik dan arsitektur untuk menghitung volume dan luas permukaan bangunan atau struktur yang berbentuk prisma segitiga.
Rumus prisma segitiga pertama kali ditemukan oleh matematikawan Yunani kuno, Euclid, pada abad ke-3 SM. Rumus ini kemudian dikembangkan lebih lanjut oleh matematikawan-matematikawan lainnya sepanjang sejarah. Saat ini, rumus prisma segitiga merupakan salah satu rumus dasar dalam geometri ruang yang diajarkan di sekolah-sekolah.
Rumus Prisma Segitiga
Rumus prisma segitiga merupakan konsep penting dalam geometri ruang yang digunakan untuk menghitung volume dan luas permukaan prisma segitiga. Berikut adalah 7 aspek penting yang terkait dengan rumus prisma segitiga:
- Definisi: Rumus untuk menghitung volume dan luas permukaan prisma segitiga.
- Bentuk: V = 1/2 luas alas tinggi dan L = 2 * (luas alas + luas selimut).
- Aplikasi: Menghitung volume dan luas permukaan bangunan, struktur, dan benda berbentuk prisma segitiga.
- Sejarah: Ditemukan oleh Euclid pada abad ke-3 SM.
- Matematika: Bagian dari geometri ruang.
- Pendidikan: Diajarkan di sekolah-sekolah.
- Relevansi: Penting dalam bidang teknik, arsitektur, dan desain.
Ketujuh aspek tersebut saling terkait dan membentuk pemahaman yang komprehensif tentang rumus prisma segitiga. Misalnya, definisi rumus memberikan dasar untuk memahami bentuknya, yang kemudian digunakan dalam aplikasi praktis. Sejarah rumus memberikan konteks tentang perkembangannya, sementara aspek matematika dan pendidikan menunjukkan pentingnya dalam pembelajaran dan pengembangan pengetahuan. Relevansinya dalam berbagai bidang menunjukkan luasnya aplikasi rumus prisma segitiga dalam kehidupan nyata.
Definisi
Definisi rumus prisma segitiga menjadi dasar untuk memahami konsep dan penerapannya. Rumus ini memberikan cara yang sistematis untuk menghitung volume dan luas permukaan prisma segitiga, yang merupakan bangun ruang tiga dimensi yang umum ditemukan di berbagai bidang kehidupan.
- Konteks dan Aplikasi
Rumus prisma segitiga sangat penting dalam berbagai bidang, seperti teknik, arsitektur, dan desain. Dalam teknik, rumus ini digunakan untuk menghitung volume dan luas permukaan struktur bangunan, jembatan, dan benda-benda lain yang berbentuk prisma segitiga. Dalam arsitektur, rumus ini digunakan untuk menghitung volume dan luas permukaan bangunan, seperti rumah, gedung, dan tempat ibadah. Dalam desain, rumus ini digunakan untuk menghitung volume dan luas permukaan benda-benda dekoratif, seperti vas bunga, lampu, dan perabot. - Pendidikan dan Pembelajaran
Rumus prisma segitiga merupakan bagian penting dari kurikulum matematika di sekolah-sekolah. Rumus ini diajarkan untuk memberikan siswa pemahaman tentang geometri ruang dan cara menghitung volume dan luas permukaan bangun ruang tiga dimensi. Pemahaman tentang rumus prisma segitiga juga membantu siswa mengembangkan keterampilan berpikir kritis dan pemecahan masalah. - Sejarah dan Perkembangan
Rumus prisma segitiga pertama kali ditemukan oleh matematikawan Yunani kuno, Euclid, pada abad ke-3 SM. Rumus ini kemudian dikembangkan lebih lanjut oleh matematikawan-matematikawan lainnya sepanjang sejarah. Perkembangan rumus prisma segitiga sejalan dengan perkembangan matematika dan geometri secara umum, yang mengarah pada pemahaman yang lebih baik tentang sifat-sifat bangun ruang dan cara menghitung volume dan luas permukaannya.
Dengan memahami definisi dan konteks rumus prisma segitiga, kita dapat memperoleh pemahaman yang lebih komprehensif tentang pentingnya dan penerapannya dalam berbagai bidang kehidupan.
Bentuk
Bentuk rumus prisma segitiga, yaitu V = 1/2 luas alas tinggi dan L = 2 (luas alas + luas selimut), merupakan representasi matematis dari sifat-sifat bangun ruang prisma segitiga. Rumus ini memberikan cara untuk menghitung volume dan luas permukaan prisma segitiga, yang merupakan besaran penting dalam berbagai bidang kehidupan.
- Volume dan Luas Permukaan
Rumus V = 1/2 luas alas tinggi digunakan untuk menghitung volume prisma segitiga, yaitu ruang yang ditempati oleh prisma segitiga tersebut. Sementara itu, rumus L = 2 * (luas alas + luas selimut) digunakan untuk menghitung luas permukaan prisma segitiga, yaitu luas seluruh permukaan prisma segitiga tersebut. - Aplikasi Praktis
Bentuk rumus prisma segitiga memiliki banyak aplikasi praktis dalam kehidupan sehari-hari. Misalnya, dalam bidang teknik dan konstruksi, rumus ini digunakan untuk menghitung volume dan luas permukaan bangunan, jembatan, dan struktur lainnya yang berbentuk prisma segitiga. Dalam bidang desain dan arsitektur, rumus ini digunakan untuk menghitung volume dan luas permukaan benda-benda seperti vas bunga, lampu, dan perabot yang berbentuk prisma segitiga. - Sifat Prisma Segitiga
Bentuk rumus prisma segitiga juga mencerminkan sifat-sifat bangun ruang prisma segitiga. Misalnya, faktor 1/2 pada rumus volume menunjukkan bahwa volume prisma segitiga adalah setengah dari volume prisma dengan alas dan tinggi yang sama. Selain itu, faktor 2 pada rumus luas permukaan menunjukkan bahwa luas permukaan prisma segitiga adalah dua kali luas alasnya ditambah luas selimutnya. - Pembelajaran Matematika
Bentuk rumus prisma segitiga juga penting dalam pembelajaran matematika, khususnya geometri ruang. Rumus ini diajarkan di sekolah-sekolah untuk memberikan siswa pemahaman tentang sifat-sifat prisma segitiga dan cara menghitung volume dan luas permukaannya.
Dengan memahami bentuk rumus prisma segitiga, kita dapat memperoleh pemahaman yang lebih baik tentang bangun ruang prisma segitiga, sifat-sifatnya, dan penerapannya dalam berbagai bidang kehidupan.
Aplikasi
Rumus prisma segitiga memiliki aplikasi yang luas dalam kehidupan nyata, khususnya dalam menghitung volume dan luas permukaan bangunan, struktur, dan benda berbentuk prisma segitiga. Aplikasi ini sangat penting dalam berbagai bidang, seperti teknik, arsitektur, dan desain.
- Teknik dan Konstruksi
Dalam bidang teknik dan konstruksi, rumus prisma segitiga digunakan untuk menghitung volume dan luas permukaan bangunan, jembatan, dan struktur lainnya yang berbentuk prisma segitiga. Misalnya, rumus ini digunakan untuk menghitung volume ruang dalam sebuah gedung atau luas permukaan dinding sebuah jembatan yang berbentuk prisma segitiga. - Arsitektur dan Desain
Dalam bidang arsitektur dan desain, rumus prisma segitiga digunakan untuk menghitung volume dan luas permukaan benda-benda seperti vas bunga, lampu, dan perabot yang berbentuk prisma segitiga. Misalnya, rumus ini digunakan untuk menghitung volume air yang dapat ditampung dalam sebuah vas bunga berbentuk prisma segitiga atau luas permukaan sebuah lampu berbentuk prisma segitiga yang perlu dicat. - Kehidupan Sehari-hari
Rumus prisma segitiga juga dapat digunakan dalam kehidupan sehari-hari untuk menghitung volume dan luas permukaan benda-benda yang berbentuk prisma segitiga, seperti kotak pensil, kardus pembungkus, dan atap rumah. Misalnya, rumus ini dapat digunakan untuk menghitung volume pensil yang dapat ditampung dalam sebuah kotak pensil berbentuk prisma segitiga atau luas permukaan atap rumah yang berbentuk prisma segitiga yang perlu diperbaiki.
Aplikasi rumus prisma segitiga dalam menghitung volume dan luas permukaan bangunan, struktur, dan benda berbentuk prisma segitiga menunjukkan pentingnya rumus ini dalam berbagai bidang kehidupan. Rumus ini memberikan cara yang sistematis dan akurat untuk menentukan volume dan luas permukaan benda-benda tersebut, yang sangat penting untuk perencanaan, konstruksi, dan desain.
Sejarah
Sejarah penemuan rumus prisma segitiga oleh Euclid pada abad ke-3 SM memainkan peran penting dalam perkembangan matematika dan geometri. Penemuan ini menjadi dasar bagi pengembangan konsep volume dan luas permukaan bangun ruang, khususnya prisma segitiga.
Euclid, seorang matematikawan Yunani kuno, dikenal sebagai “Bapak Geometri” karena kontribusinya yang luar biasa dalam bidang geometri. Dalam karyanya yang terkenal, “Elements”, Euclid menyajikan rumus prisma segitiga beserta bukti matematisnya. Rumus ini menjadi landasan bagi pemahaman tentang sifat-sifat prisma segitiga dan cara menghitung volume dan luas permukaannya.
Penemuan rumus prisma segitiga oleh Euclid memiliki dampak yang signifikan pada perkembangan matematika. Rumus ini menjadi alat penting dalam berbagai bidang, seperti teknik, arsitektur, dan desain. Rumus ini juga menjadi dasar bagi pengembangan konsep volume dan luas permukaan bangun ruang lainnya, seperti limas, kerucut, dan bola.
Matematika
Rumus prisma segitiga merupakan bagian dari geometri ruang, cabang matematika yang mempelajari bangun-bangun ruang tiga dimensi. Geometri ruang sangat penting dalam kehidupan sehari-hari, digunakan dalam berbagai bidang seperti arsitektur, teknik, dan desain.
- Konsep Geometri Ruang
Geometri ruang mempelajari sifat-sifat dan hubungan bangun-bangun ruang, seperti prisma segitiga. Konsep-konsep seperti volume dan luas permukaan sangat penting dalam geometri ruang dan memiliki aplikasi luas dalam kehidupan nyata. - Aplikasi dalam Arsitektur
Arsitek menggunakan rumus prisma segitiga untuk menghitung volume dan luas permukaan bangunan, seperti rumah dan gedung. Hal ini penting untuk memastikan stabilitas struktural dan efisiensi ruang. - Aplikasi dalam Teknik
Insinyur menggunakan rumus prisma segitiga untuk menghitung volume dan luas permukaan struktur, seperti jembatan dan bendungan. Perhitungan yang akurat sangat penting untuk memastikan keamanan dan daya tahan struktur. - Aplikasi dalam Desain
Desainer menggunakan rumus prisma segitiga untuk menghitung volume dan luas permukaan benda-benda, seperti furnitur dan peralatan rumah tangga. Hal ini penting untuk memastikan fungsionalitas dan estetika desain.
Dengan memahami hubungan antara rumus prisma segitiga dan geometri ruang, kita dapat lebih menghargai pentingnya dan penerapannya dalam berbagai bidang kehidupan. Geometri ruang menyediakan dasar matematika untuk menghitung volume dan luas permukaan bangun ruang, termasuk prisma segitiga, yang sangat penting untuk desain, konstruksi, dan banyak aspek kehidupan lainnya.
Pendidikan
Rumus prisma segitiga merupakan bagian penting dari kurikulum matematika yang diajarkan di sekolah-sekolah. Pengajaran rumus ini bertujuan untuk membekali siswa dengan pemahaman tentang bangun ruang tiga dimensi, khususnya prisma segitiga, serta cara menghitung volume dan luas permukaannya.
- Pemahaman Bangun Ruang
Melalui pembelajaran rumus prisma segitiga, siswa memperoleh pemahaman tentang konsep bangun ruang tiga dimensi. Mereka belajar tentang sifat-sifat prisma segitiga, seperti memiliki dua sisi yang sejajar dan kongruen, serta cara mengidentifikasi dan membedakannya dari bangun ruang lainnya. - Penerapan dalam Kehidupan Nyata
Pengajaran rumus prisma segitiga juga mengajarkan siswa tentang penerapannya dalam kehidupan nyata. Mereka belajar bahwa rumus ini dapat digunakan untuk menghitung volume dan luas permukaan berbagai benda berbentuk prisma segitiga, seperti kotak pensil, kemasan makanan, dan atap rumah. Hal ini membantu siswa memahami relevansi matematika dalam kehidupan sehari-hari. - Keterampilan Berpikir Kritis
Proses mempelajari dan menerapkan rumus prisma segitiga juga mengembangkan keterampilan berpikir kritis siswa. Mereka belajar memecah masalah, menganalisis informasi, dan menggunakan penalaran logis untuk menyelesaikan soal-soal yang berkaitan dengan volume dan luas permukaan prisma segitiga. Keterampilan ini sangat penting untuk kesuksesan dalam matematika dan bidang lainnya. - Kesiapan untuk Pendidikan Tinggi dan Karier
Pemahaman tentang rumus prisma segitiga merupakan dasar penting untuk pendidikan tinggi dan karier di bidang sains, teknologi, teknik, dan matematika (STEM). Siswa yang memiliki pemahaman yang kuat tentang konsep ini akan lebih siap untuk melanjutkan studi mereka dalam bidang-bidang tersebut dan untuk memecahkan masalah yang melibatkan geometri ruang dalam kehidupan profesional mereka.
Dengan demikian, pengajaran rumus prisma segitiga di sekolah-sekolah memainkan peran penting dalam membekali siswa dengan pemahaman tentang bangun ruang tiga dimensi, keterampilan berpikir kritis, dan kesiapan untuk pendidikan tinggi dan karier di bidang STEM. Pemahaman tentang rumus ini sangat penting untuk literasi matematika dan aplikasi praktis dalam berbagai bidang kehidupan.
Relevansi
Rumus prisma segitiga memiliki relevansi yang tinggi dalam bidang teknik, arsitektur, dan desain karena perannya dalam menghitung volume dan luas permukaan benda-benda berbentuk prisma segitiga. Pemahaman tentang rumus ini sangat penting untuk memastikan stabilitas, efisiensi, dan estetika struktur dan benda yang dirancang.
- Teknik Sipil
Dalam teknik sipil, rumus prisma segitiga digunakan untuk menghitung volume dan luas permukaan struktur seperti jembatan, bendungan, dan gedung. Perhitungan yang akurat sangat penting untuk memastikan stabilitas dan keamanan struktur, serta untuk mengoptimalkan penggunaan bahan dan biaya konstruksi. - Arsitektur
Arsitek menggunakan rumus prisma segitiga untuk menghitung volume dan luas permukaan bangunan, seperti rumah, sekolah, dan gedung perkantoran. Perhitungan ini penting untuk menentukan kebutuhan ruang, pencahayaan, dan ventilasi yang memadai, serta untuk memperkirakan biaya pembangunan. - Desain Industri
Dalam desain industri, rumus prisma segitiga digunakan untuk menghitung volume dan luas permukaan produk seperti furnitur, peralatan rumah tangga, dan kemasan. Perhitungan ini penting untuk memastikan fungsionalitas, estetika, dan efisiensi penggunaan bahan dalam desain produk. - Desain Grafis
Meskipun tidak secara langsung menghitung volume dan luas permukaan, rumus prisma segitiga dapat digunakan dalam desain grafis untuk membuat representasi visual dari benda-benda berbentuk prisma segitiga. Representasi ini penting untuk visualisasi dan komunikasi desain, seperti dalam pembuatan brosur, poster, dan kemasan produk.
Relevansi rumus prisma segitiga dalam bidang teknik, arsitektur, dan desain menunjukkan pentingnya memahami dan menerapkan rumus ini untuk menciptakan struktur dan benda yang fungsional, estetis, dan aman. Rumus ini merupakan alat penting bagi para profesional di bidang-bidang tersebut untuk memastikan kualitas dan keberhasilan proyek-proyek mereka.
Pertanyaan yang Sering Diajukan
Berikut adalah beberapa pertanyaan yang sering diajukan mengenai rumus prisma segitiga:
Pertanyaan 1: Apa saja rumus untuk menghitung volume dan luas permukaan prisma segitiga?
Jawaban:Rumus untuk menghitung volume prisma segitiga adalah V = 1/2 luas alas tinggi. Sedangkan rumus untuk menghitung luas permukaan prisma segitiga adalah L = 2 * (luas alas + luas selimut).
Pertanyaan 2: Dalam bidang apa saja rumus prisma segitiga digunakan?
Jawaban:Rumus prisma segitiga banyak digunakan dalam bidang teknik, arsitektur, dan desain untuk menghitung volume dan luas permukaan benda-benda berbentuk prisma segitiga.
Pertanyaan 3: Mengapa penting mempelajari rumus prisma segitiga?
Jawaban:Mempelajari rumus prisma segitiga penting karena rumus ini memberikan cara sistematis untuk menghitung volume dan luas permukaan benda-benda berbentuk prisma segitiga, yang merupakan bangun ruang yang umum ditemukan dalam kehidupan sehari-hari.
Pertanyaan 4: Bagaimana rumus prisma segitiga ditemukan?
Jawaban:Rumus prisma segitiga pertama kali ditemukan oleh matematikawan Yunani kuno, Euclid, pada abad ke-3 SM.
Mengetahui jawaban atas pertanyaan-pertanyaan ini dapat membantu kita memahami pentingnya dan penerapan rumus prisma segitiga dalam berbagai bidang kehidupan.
Untuk informasi lebih lanjut, silakan baca artikel lengkap di bawah ini.
Tips Memahami Rumus Prisma Segitiga
Memahami rumus prisma segitiga sangat penting dalam geometri ruang. Berikut adalah beberapa tips untuk mempermudah pemahaman:
Tip 1: Pahami Konsep Bangun Ruang
Pahami terlebih dahulu konsep bangun ruang, khususnya prisma segitiga. Identifikasi ciri-ciri khas prisma segitiga, seperti memiliki dua sisi yang sejajar dan kongruen.
Tip 2: Visualisasikan Rumus
Bayangkan bangun ruang prisma segitiga dan rumusnya secara visual. Hubungkan setiap bagian rumus dengan konsep geometri prisma segitiga, seperti luas alas, tinggi, dan luas selimut.
Tip 3: Latihan Soal
Kerjakan soal-soal latihan sebanyak mungkin. Latihan akan meningkatkan pemahaman dan kemampuan menerapkan rumus dalam berbagai situasi.
Tip 4: Hubungkan dengan Kehidupan Nyata
Cari contoh penerapan rumus prisma segitiga dalam kehidupan nyata, seperti menghitung volume kotak pensil atau luas permukaan atap rumah. Hal ini akan memperkuat pemahaman tentang pentingnya rumus.
Tip 5: Manfaatkan Teknologi
Gunakan kalkulator atau aplikasi matematika untuk melakukan perhitungan. Namun, pastikan untuk tetap memahami konsep dan rumus yang digunakan.
Tip 6: Cari Bantuan
Jangan ragu untuk bertanya kepada guru, teman, atau sumber belajar lainnya jika mengalami kesulitan memahami rumus prisma segitiga.
Tip 7: Uji Pemahaman
Setelah mempelajari rumus dan tips di atas, uji pemahaman dengan mengerjakan soal-soal yang lebih kompleks atau menjelaskan konsep kepada orang lain.
Tip 8: Konsistensi dan Ketekunan
Memahami rumus prisma segitiga membutuhkan konsistensi dan ketekunan. Teruslah berlatih dan jangan menyerah jika mengalami kesulitan.
Dengan mengikuti tips ini, Anda dapat meningkatkan pemahaman tentang rumus prisma segitiga dan menerapkannya dengan lebih efektif dalam berbagai situasi.
Selain tips di atas, disarankan untuk membaca artikel lengkap tentang rumus prisma segitiga untuk pemahaman yang lebih komprehensif.
Youtube Video: