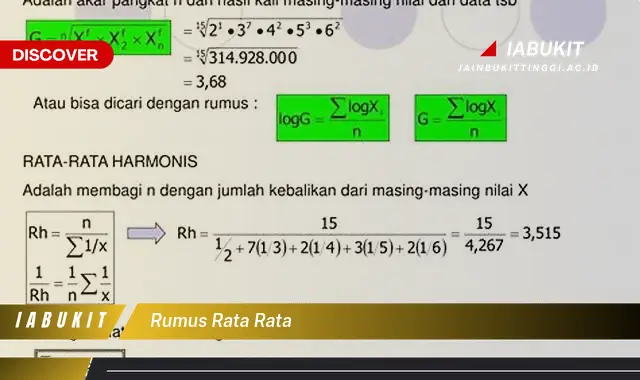
Rumus rata-rata adalah suatu cara untuk menghitung nilai rata-rata dari suatu kumpulan data. Rumus ini digunakan untuk mengetahui nilai tengah dari suatu data yang diambil dari suatu himpunan. Secara umum, rumus rata-rata dapat dihitung dengan menjumlahkan seluruh nilai data kemudian dibagi dengan banyaknya data.
Rumus rata-rata sangat penting dalam statistika dan banyak digunakan dalam berbagai bidang, seperti penelitian, bisnis, dan pendidikan. Rumus ini memungkinkan kita untuk meringkas dan membandingkan kumpulan data yang besar, serta membuat keputusan berdasarkan data tersebut. Selain itu, rumus rata-rata juga membantu kita dalam memahami tren dan pola dalam suatu data.
Rumus rata-rata memiliki sejarah panjang dan telah digunakan selama berabad-abad. Seiring dengan perkembangan matematika, rumus rata-rata terus diperluas dan disempurnakan untuk memenuhi kebutuhan analisis data yang semakin kompleks.
Rumus Rata-Rata
Rumus rata-rata merupakan konsep penting dalam statistika yang digunakan untuk meringkas dan menganalisis data. Rumus ini memiliki beberapa aspek penting yang perlu dipahami:
- Definisi: Rumus untuk menghitung nilai tengah dari suatu kumpulan data.
- Jenis: Ada berbagai jenis rumus rata-rata, seperti mean, median, dan modus.
- Aplikasi: Digunakan dalam berbagai bidang, seperti penelitian, bisnis, dan pendidikan.
- Interpretasi: Membantu memahami tren dan pola dalam suatu data.
- Sejarah: Telah digunakan selama berabad-abad dan terus berkembang.
- Keterbatasan: Dapat dipengaruhi oleh nilai ekstrem (outlier) dalam data.
- Pentingnya: Memungkinkan pengambilan keputusan berdasarkan data yang lebih akurat.
Rumus rata-rata saling berkaitan dan melengkapi satu sama lain. Misalnya, mean (rata-rata aritmatika) memberikan gambaran umum tentang nilai tengah data, sedangkan median (rata-rata tengah) tidak terpengaruh oleh nilai ekstrem. Memahami aspek-aspek ini sangat penting untuk menggunakan rumus rata-rata secara efektif dalam menganalisis data.
Definisi
Definisi ini menjelaskan bahwa rumus rata-rata adalah sebuah cara untuk menghitung nilai tengah dari suatu kumpulan data. Nilai tengah ini mewakili nilai yang berada di tengah-tengah data yang telah diurutkan dari yang terkecil ke terbesar. Rumus ini menjadi dasar untuk berbagai jenis rata-rata, seperti mean, median, dan modus.
- Jenis-jenis Rata-rata
Rumus rata-rata memiliki beberapa jenis, yaitu mean, median, dan modus. Mean adalah rata-rata aritmatika yang dihitung dengan menjumlahkan semua nilai data kemudian dibagi dengan jumlah data. Median adalah nilai tengah dari data yang telah diurutkan. Modus adalah nilai yang paling sering muncul dalam suatu kumpulan data.
- Aplikasi dalam Kehidupan Nyata
Rumus rata-rata digunakan dalam berbagai bidang kehidupan nyata, seperti:
– Penelitian: Untuk menganalisis data eksperimen dan survei.
– Bisnis: Untuk menghitung rata-rata penjualan, biaya, dan keuntungan.
– Pendidikan: Untuk menghitung nilai rata-rata siswa. - Implikasi dalam Konteks “Rumus Rata Rata”
Definisi ini memberikan landasan dasar untuk memahami rumus rata-rata. Dengan mengetahui bahwa rumus rata-rata digunakan untuk menghitung nilai tengah dari suatu kumpulan data, kita dapat lebih mudah memahami konsep dan aplikasi dari rumus rata-rata.
Kesimpulannya, definisi ini memberikan pemahaman yang mendasar tentang konsep rumus rata-rata dan jenis-jenisnya. Definisi ini juga menyoroti aplikasi praktis dari rumus rata-rata dalam berbagai bidang kehidupan nyata, sehingga memperkuat relevansinya dan memperluas pemahaman kita tentang topik ini.
Jenis
Pernyataan ini menjelaskan bahwa rumus rata-rata memiliki beberapa jenis, yaitu mean, median, dan modus. Masing-masing jenis rumus rata-rata ini memiliki karakteristik dan kegunaan yang berbeda, sehingga penting untuk memahami perbedaannya.
Mean, atau rata-rata aritmatika, dihitung dengan menjumlahkan semua nilai data dan membaginya dengan jumlah data. Mean memberikan gambaran tentang nilai rata-rata secara keseluruhan, namun dapat dipengaruhi oleh nilai ekstrem (outlier) dalam data.
Median, atau rata-rata tengah, adalah nilai yang berada di tengah-tengah data ketika diurutkan dari yang terkecil ke terbesar. Median tidak terpengaruh oleh nilai ekstrem, sehingga lebih stabil dibandingkan mean.
Modus adalah nilai yang paling sering muncul dalam suatu kumpulan data. Modus memberikan gambaran tentang nilai yang paling umum atau dominan dalam data.
Ketiga jenis rumus rata-rata ini saling melengkapi dan digunakan dalam situasi yang berbeda. Memahami perbedaan dan kegunaan masing-masing jenis rumus rata-rata sangat penting untuk menganalisis dan menginterpretasikan data secara efektif.
Aplikasi
Rumus rata-rata memiliki banyak aplikasi dalam berbagai bidang karena kemampuannya untuk meringkas dan menganalisis data. Berikut adalah beberapa bidang utama di mana rumus rata-rata digunakan:
- Penelitian: Dalam penelitian, rumus rata-rata digunakan untuk menganalisis data eksperimen dan survei. Misalnya, peneliti dapat menggunakan mean untuk menghitung nilai rata-rata skor tes atau median untuk membandingkan dua kelompok.
- Bisnis: Dalam bisnis, rumus rata-rata digunakan untuk menghitung rata-rata penjualan, biaya, dan keuntungan. Informasi ini dapat digunakan untuk membuat keputusan bisnis yang tepat, seperti menentukan harga produk atau merencanakan strategi pemasaran.
- Pendidikan: Dalam pendidikan, rumus rata-rata digunakan untuk menghitung nilai rata-rata siswa. Informasi ini dapat digunakan untuk mengevaluasi kinerja siswa dan memberikan umpan balik yang tepat.
Aplikasi rumus rata-rata dalam berbagai bidang ini menunjukkan pentingnya dan relevansinya dalam dunia nyata. Dengan memahami cara menggunakan rumus rata-rata secara efektif, kita dapat memperoleh wawasan yang berharga dari data dan membuat keputusan yang lebih tepat berdasarkan informasi.
Interpretasi
Interpretasi memegang peranan penting dalam rumus rata-rata karena memungkinkan kita untuk memperoleh makna dan wawasan dari data yang dianalisis. Dengan memahami tren dan pola dalam suatu data, kita dapat membuat prediksi dan mengambil keputusan yang lebih tepat.
- Mengidentifikasi Tren
Rumus rata-rata membantu mengidentifikasi tren dalam data dengan menunjukkan nilai rata-rata dari waktu ke waktu. Misalnya, dalam bisnis, perusahaan dapat menggunakan rumus rata-rata untuk melacak tren penjualan dan mengidentifikasi periode puncak dan lembah.
- Mendeteksi Pola
Rumus rata-rata juga dapat digunakan untuk mendeteksi pola dalam data. Misalnya, dalam penelitian medis, rumus rata-rata dapat digunakan untuk mengidentifikasi pola penyebaran penyakit atau efektivitas pengobatan.
- Membuat Prediksi
Dengan memahami tren dan pola dalam data, rumus rata-rata dapat digunakan untuk membuat prediksi tentang perilaku atau kejadian di masa depan. Misalnya, dalam meteorologi, rumus rata-rata dapat digunakan untuk memprediksi cuaca berdasarkan data historis.
- Mengambil Keputusan
Interpretasi yang tepat terhadap tren dan pola dalam data sangat penting untuk mengambil keputusan yang tepat. Misalnya, dalam manajemen keuangan, rumus rata-rata dapat digunakan untuk mengevaluasi kinerja investasi dan membuat keputusan investasi yang lebih baik.
Kesimpulannya, interpretasi tren dan pola dalam suatu data merupakan aspek penting dari rumus rata-rata. Dengan memahami cara menggunakan rumus rata-rata secara efektif, kita dapat memperoleh wawasan yang berharga dari data dan membuat keputusan yang lebih tepat berdasarkan informasi.
Sejarah
Sejarah rumus rata-rata sangat panjang dan menarik. Rumus ini telah digunakan selama berabad-abad untuk meringkas dan menganalisis data, dan terus berkembang seiring dengan kemajuan matematika.
- Akar Kuno
Konsep rata-rata telah ada sejak zaman kuno. Bangsa Babilonia dan Mesir Kuno menggunakan metode sederhana untuk menghitung rata-rata, seperti menjumlahkan nilai dan membaginya dengan jumlah nilai.
- Perkembangan Matematika
Pada abad pertengahan, matematikawan Muslim mengembangkan metode yang lebih canggih untuk menghitung rata-rata. Mereka memperkenalkan konsep mean, median, dan modus, yang masih digunakan hingga saat ini.
- Revolusi Ilmiah
Selama Revolusi Ilmiah, rumus rata-rata memainkan peran penting dalam perkembangan statistika. Ilmuwan seperti Galileo Galilei dan Isaac Newton menggunakan rumus rata-rata untuk menganalisis data eksperimen dan membuat penemuan ilmiah.
- Era Modern
Pada era modern, rumus rata-rata terus berkembang dengan perkembangan komputer dan teknologi. Saat ini, rumus rata-rata dapat dihitung dengan mudah menggunakan kalkulator atau perangkat lunak statistik.
Perkembangan sejarah rumus rata-rata menunjukkan pentingnya dan relevansinya dalam menganalisis data. Rumus ini telah digunakan selama berabad-abad untuk memahami tren, pola, dan hubungan dalam data, dan terus menjadi alat penting dalam berbagai bidang.
Keterbatasan
Keterbatasan ini menjadi pertimbangan penting dalam penggunaan rumus rata-rata. Nilai ekstrem, atau outlier, adalah nilai data yang sangat berbeda dari nilai lainnya dalam suatu kumpulan data. Kehadiran outlier dapat mempengaruhi nilai rata-rata, sehingga memberikan gambaran yang kurang akurat tentang nilai tengah sebenarnya dari data.
- Dampak pada Mean
Mean, atau rata-rata aritmatika, sangat rentan terhadap pengaruh outlier. Nilai ekstrem yang sangat tinggi atau rendah dapat menarik nilai rata-rata menjauh dari nilai tengah sebenarnya. Misalnya, jika kita memiliki kumpulan data pendapatan dengan satu individu yang berpenghasilan sangat tinggi, mean akan lebih tinggi dari pendapatan rata-rata sebenarnya dari seluruh kelompok.
- Median Lebih Stabil
Median, atau rata-rata tengah, tidak terpengaruh oleh nilai ekstrem. Median tetap menjadi nilai tengah data, bahkan ketika ada outlier. Oleh karena itu, median sering digunakan sebagai ukuran rata-rata yang lebih stabil ketika terdapat outlier dalam data.
- Mempertimbangkan Konteks
Saat menggunakan rumus rata-rata, penting untuk mempertimbangkan konteks data dan keberadaan outlier. Jika terdapat outlier yang dapat mempengaruhi nilai rata-rata secara signifikan, perlu dilakukan analisis lebih lanjut untuk memahami dampaknya terhadap interpretasi data.
Keterbatasan ini menekankan pentingnya memahami sifat data dan memilih jenis rata-rata yang sesuai. Dengan mempertimbangkan potensi pengaruh outlier, kita dapat menggunakan rumus rata-rata secara efektif untuk menganalisis dan menginterpretasikan data dengan lebih akurat.
Pentingnya
Rumus rata-rata memegang peranan penting dalam pengambilan keputusan yang akurat karena memberikan representasi data yang ringkas dan bermakna. Dengan menggunakan rumus rata-rata, kita dapat mengidentifikasi tren, pola, dan hubungan dalam data, yang kemudian dapat digunakan sebagai dasar untuk pengambilan keputusan yang tepat.
Misalnya, dalam dunia bisnis, rumus rata-rata dapat digunakan untuk menganalisis data penjualan dan mengidentifikasi produk yang paling diminati pelanggan. Informasi ini dapat digunakan untuk membuat keputusan yang tepat tentang strategi pemasaran dan pengembangan produk.
Selain itu, rumus rata-rata juga penting dalam penelitian ilmiah. Dengan menghitung rata-rata hasil eksperimen, peneliti dapat menarik kesimpulan yang lebih akurat dan andal. Misalnya, dalam penelitian medis, rumus rata-rata dapat digunakan untuk menentukan efektivitas pengobatan baru dengan membandingkan hasil kelompok yang menerima pengobatan dengan kelompok kontrol.
Kesimpulannya, rumus rata-rata merupakan alat yang sangat penting untuk pengambilan keputusan yang akurat karena memungkinkan kita untuk mengolah dan memahami data secara efektif. Dengan menggunakan rumus rata-rata, kita dapat membuat keputusan yang tepat berdasarkan informasi yang lebih komprehensif dan andal.
Pertanyaan Umum tentang Rumus Rata-Rata
Berikut adalah beberapa pertanyaan umum dan jawabannya terkait rumus rata-rata:
Pertanyaan 1: Apa saja jenis-jenis rumus rata-rata?
Jawaban: Ada beberapa jenis rumus rata-rata, yang paling umum adalah mean (rata-rata aritmatika), median (rata-rata tengah), dan modus (nilai yang paling sering muncul).
Pertanyaan 2: Bagaimana cara menghitung mean?
Jawaban: Mean dihitung dengan menjumlahkan semua nilai data dan membaginya dengan jumlah data.
Pertanyaan 3: Apa perbedaan antara mean dan median?
Jawaban: Mean dipengaruhi oleh nilai ekstrem (outlier), sedangkan median tidak. Median lebih stabil dan menjadi ukuran rata-rata yang lebih baik ketika terdapat outlier dalam data.
Pertanyaan 4: Kapan sebaiknya menggunakan rumus rata-rata?
Jawaban: Rumus rata-rata digunakan ketika kita ingin meringkas dan menganalisis data untuk mengidentifikasi tren, pola, dan hubungan. Rumus ini banyak digunakan dalam penelitian, bisnis, dan pendidikan.
Kesimpulannya, rumus rata-rata adalah alat penting untuk menganalisis data dan mengambil keputusan yang tepat. Dengan memahami jenis-jenis rumus rata-rata dan cara menggunakannya secara efektif, kita dapat memperoleh wawasan yang berharga dari data dan membuat keputusan yang lebih baik berdasarkan informasi.
Artikel Berikutnya: Aplikasi Rumus Rata-Rata dalam Berbagai Bidang
Tips untuk Menggunakan Rumus Rata-Rata Secara Efektif
Rumus rata-rata merupakan alat penting untuk menganalisis data dan memperoleh wawasan yang berharga. Berikut beberapa tips untuk menggunakan rumus rata-rata secara efektif:
Tip 1: Tentukan Jenis Rata-Rata yang TepatPilih jenis rata-rata yang sesuai dengan tujuan analisis dan sifat data. Mean cocok untuk data yang terdistribusi normal, sedangkan median lebih stabil ketika terdapat nilai ekstrem (outlier).
Tip 2: Perhatikan Ukuran SampelUkuran sampel yang lebih besar umumnya menghasilkan rata-rata yang lebih akurat. Pastikan ukuran sampel cukup besar untuk mewakili populasi yang lebih luas.
Tip 3: Identifikasi dan Tangani OutlierNilai ekstrem (outlier) dapat mempengaruhi rata-rata, terutama mean. Identifikasi outlier dan pertimbangkan untuk menghapusnya atau menggunakan median sebagai alternatif.
Tip 4: Visualisasikan DataGunakan grafik atau bagan untuk memvisualisasikan data sebelum menghitung rata-rata. Visualisasi dapat membantu mengidentifikasi tren, pola, dan outlier yang mungkin tidak terlihat pada pandangan pertama.
Tip 5: Interpretasikan Hasil dengan Hati-hatiRata-rata hanyalah salah satu cara untuk meringkas data. Pertimbangkan konteks dan distribusi data saat menginterpretasikan hasil. Hindari membuat generalisasi yang terlalu luas berdasarkan rata-rata saja.
Tip 6: Gunakan Alat StatistikBanyak perangkat lunak statistik menyediakan fungsi untuk menghitung rata-rata dan jenis statistik lainnya. Manfaatkan alat ini untuk menghemat waktu dan meningkatkan akurasi.
Dengan mengikuti tips ini, Anda dapat menggunakan rumus rata-rata secara efektif untuk menganalisis data dan membuat keputusan yang tepat berdasarkan informasi.
Kesimpulannya, rumus rata-rata merupakan alat penting untuk menganalisis data dan memperoleh wawasan yang berharga. Dengan memahami jenis rata-rata, memperhatikan ukuran sampel, mengidentifikasi outlier, memvisualisasikan data, menginterpretasikan hasil dengan hati-hati, dan memanfaatkan alat statistik, Anda dapat menggunakan rumus rata-rata secara efektif untuk membuat keputusan yang lebih baik berdasarkan informasi.
Youtube Video: